投影一般指高维向量到低维向量的转换,在绘制管线中投影矩阵是很重要的概念,它将相机坐标系下的三维点转换成二维坐标。主流绘制引擎和工具库中都提供了通过指定相机参数(fov, aspect, 视锥参数等)来控制三维投影的方法,所以投影的数学过程常常被忽略,本文我们来推导一下投影矩阵的公式。
太长不看
给定视锥参数$l,r,t,b,n,f$,则正交投影矩阵$P_{ortho}$和透视投影矩阵$P_{persp}$分别为
$$
P_{ortho}
=
\begin{bmatrix}
\frac {2}{r - l} & 0 & 0 & -\frac {r + l}{r - l}\\
0 & \frac {2}{t - b} & 0 & -\frac {t + b}{t - b}\\
0 & 0 & \frac {2}{n - f} & -\frac {f + n}{f - n}\\
0 & 0 & 0 & 1
\end{bmatrix}
$$
$$
P_{persp}
=
\begin{bmatrix}
\frac {2n}{r - l} & 0 & -\frac {(r + l)}{r - l} & 0\\
0 & \frac {2n}{t - b} & -\frac {(t + b)}{t - b} & 0\\
0 & 0 & \frac {f + n}{f - n} & -\frac {2nf}{f - n}\\
0 & 0 & 1 & 0
\end{bmatrix}
$$
投影矩阵的推导本文参考了闫令琪在GAMES101中的思路,先推正交,再由正交推透视。
正交投影推导
参考课程讲义p22
正交投影的视锥是一个立方体,定义其左右上下前后$l,r,t,b,n,f$参数如下图
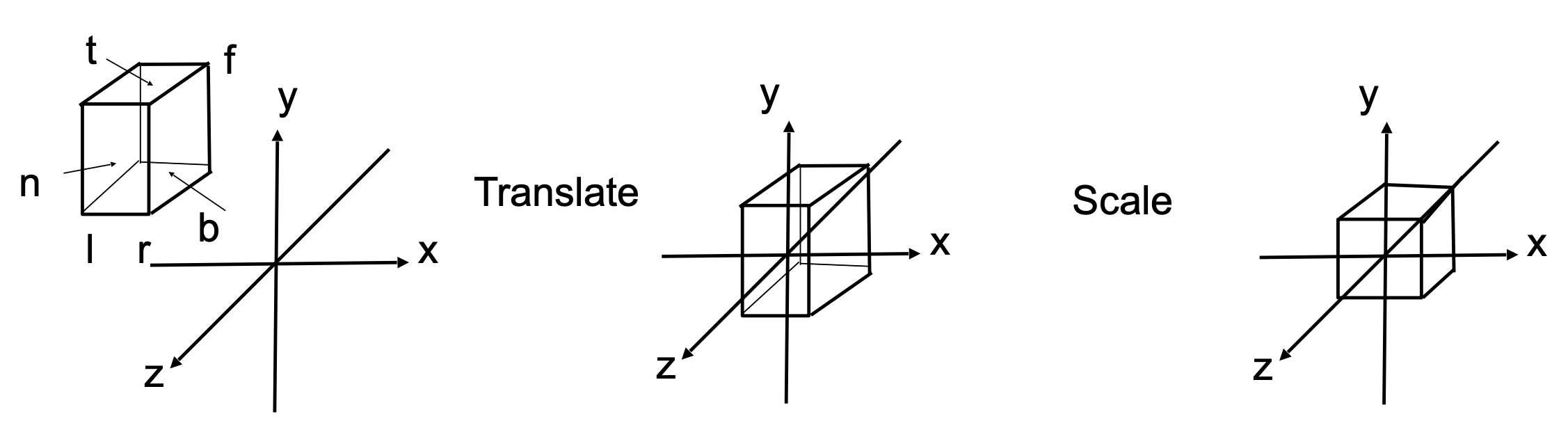
将这个立方体内的点转换成标准立方体内的点需要做两部操作,首先平移到原点,然后在三个轴上进行缩放,易得
$$
P_{ortho} = \begin{bmatrix}
\frac {2}{r - l} & 0 & 0 & 0\\
0 & \frac {2}{t - b} & 0 & 0\\
0 & 0 & \frac {2}{f - n} & 0\\
0 & 0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 & -\frac {r + l}{2}\\
0 & 1 & 0 & -\frac {t + b}{2}\\
0 & 0 & 1 & -\frac {f + n}{2}\\
0 & 0 & 0 & 1
\end{bmatrix}
=
\begin{bmatrix}
\frac {2}{r - l} & 0 & 0 & -\frac {r + l}{r - l}\\
0 & \frac {2}{t - b} & 0 & -\frac {t + b}{t - b}\\
0 & 0 & \frac {2}{n - f} & -\frac {f + n}{f - n}\\
0 & 0 & 0 & 1
\end{bmatrix}
$$
特别的,当视锥正对原点左右对称时,即满足$r=-l$和$t=-b$时,假设$w=r-l$,$h=t-b$,则上面的投影矩阵可以简化为
$$
P_{ortho} = \begin{bmatrix}
\frac {2}{w} & 0 & 0 & 0\\
0 & \frac {2}{h} & 0 & 0\\
0 & 0 & \frac {2}{f - n} & -\frac {f + n}{f - n}\\
0 & 0 & 0 & 1
\end{bmatrix}
$$
透视投影推导
参考课程讲义p29
我们已经推导了正交投影的公式,这里我们尝试推导一个4x4的变换矩阵$M_{p2o}$,将透视投影视锥中的点转换到正交投影到视锥(立方体)中,透视视锥到透视视锥的变换如下图所示

我们总结四个重要的结论,用于后面的推导:
- 结论1:在齐次坐标中有一点$P=\begin{bmatrix}x,y,z,1\end{bmatrix}^T$,n为任意数,$P^{‘}=\begin{bmatrix}nx,ny,nz,n\end{bmatrix}^T$和$P$和$P^{‘}$表示的是三维空间中的同一个点,可以说$P$和$P^{‘}$等价,记做$P==P^{‘}$
- 结论2:透视视锥内的任意点变换前后z值不变
- 结论3:透视视锥中近平面上的任意点变换前后不变
- 结论4:远平面中心点变换前后不变
先看一个基本情况,对$P=\begin{bmatrix}x,y,z,1\end{bmatrix}^T$进行变换得到$P^{‘}=\begin{bmatrix}x^{‘},y^{‘},z^{‘},1\end{bmatrix}^T$
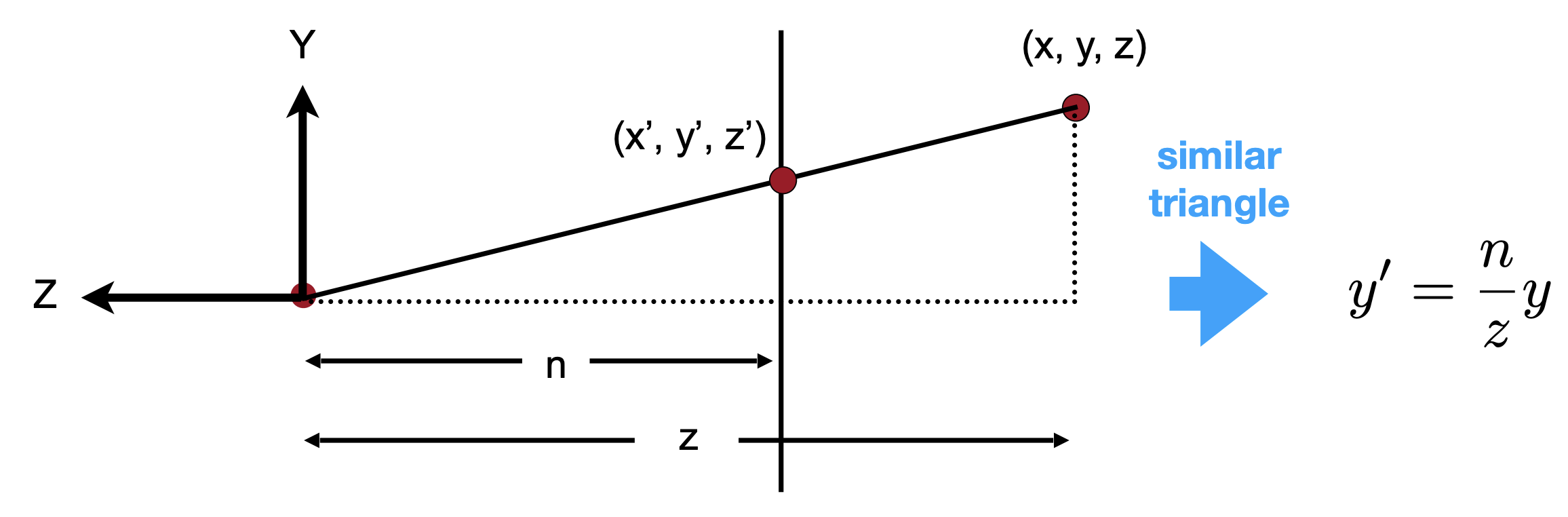
根据相似三角形原理,易得
$$
x^{‘} = \frac {nx}{z}, y^{‘} = \frac {ny}{z}
$$
根据结论1,则
$$
M_{p2o}
\begin{bmatrix}
x\\
y\\
z\\
1
\end{bmatrix}
=
\begin{bmatrix}
\frac {nx}{z}\\
\frac {ny}{z}\\
…\\
1
\end{bmatrix}
==
\begin{bmatrix}
nx\\
ny\\
…\\
z
\end{bmatrix}
$$
这一步足够求出矩阵$M_{p2o}$的第1、2、4行
$$
M_{p2o}=
\begin{bmatrix}
n & 0 & 0 & 0\\
0 & n & 0 & 0\\
… & … & … & …\\
0 & 0 & 1 & 0
\end{bmatrix}
$$
接下来我们尝试求解矩阵$M_{p2o}$的第三行,根据结论3我们可求得
$$
\begin{bmatrix}
n & 0 & 0 & 0\\
0 & n & 0 & 0\\
… & … & … & …\\
0 & 0 & 1 & 0
\end{bmatrix}
\begin{bmatrix}
x\\
y\\
n\\
1
\end{bmatrix}
=
\begin{bmatrix}
x\\
y\\
n\\
1
\end{bmatrix}
==
\begin{bmatrix}
nx\\
ny\\
n^2\\
n
\end{bmatrix}
$$
则第三行必为$[0,0,A,B]$,满足$An+B=n^2$,两个变量一个等式求不出来,我们再基于结论4,得出
$$
\begin{bmatrix}
n & 0 & 0 & 0\\
0 & n & 0 & 0\\
0 & 0 & A & B\\
0 & 0 & 1 & 0
\end{bmatrix}
\begin{bmatrix}
0\\
0\\
f\\
1
\end{bmatrix}
=
\begin{bmatrix}
0\\
0\\
f\\
1
\end{bmatrix}
==
\begin{bmatrix}
0\\
0\\
f^2\\
f
\end{bmatrix}
$$
我们可得$Af+B=f^2$,与$An+B=n^2$连立求解得$A=f+n,B=-nf$,则求解矩阵$M_{p2o}$为
$$
M_{p2o}
=
\begin{bmatrix}
n & 0 & 0 & 0\\
0 & n & 0 & 0\\
0 & 0 & f + n & -nf\\
0 & 0 & 1 & 0
\end{bmatrix}
$$
则可以求的最终的透视投影矩阵$P_{persp}$为
$$
P_{persp}
=
P_{ortho}
M_{p2o}
=
\begin{bmatrix}
\frac {2}{r - l} & 0 & 0 & -\frac {r + l}{r - l}\\
0 & \frac {2}{t - b} & 0 & -\frac {t + b}{t - b}\\
0 & 0 & \frac {2}{f - n} & -\frac {f + n}{f - n}\\
0 & 0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
n & 0 & 0 & 0\\
0 & n & 0 & 0\\
0 & 0 & f+n & -nf\\
0 & 0 & 1 & 0
\end{bmatrix}
\\=
\begin{bmatrix}
\frac {2n}{r - l} & 0 & -\frac {(r + l)}{r - l} & 0\\
0 & \frac {2n}{t - b} & -\frac {(t + b)}{t - b} & 0\\
0 & 0 & \frac {f + n}{f - n} & -\frac {2nf}{f - n}\\
0 & 0 & 1 & 0
\end{bmatrix}
$$
参考