左右手坐标系下旋转平移的转换
太长不看
假设右(或左)手坐标系下的旋转矩阵和平移向量分别为$R$和$T$,左(或右)手坐标系下分别为$R^{’}$和$T^{’}$,假设$S = \begin{bmatrix}
-1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{bmatrix}$,则有
$$
R = S \cdot R^{’} \cdot S \\
T = S \cdot T^{’}
$$
推导
右手食指为Y轴正方向,中指为Z轴正方向,大拇指为X轴正方向,这样的坐标系为右手坐标系。右手换成左手则为左手坐标系。将一个坐标系的一个轴取反向,则改变了手性;两个轴取反向,则等价于绕第三轴旋转180度;将三个轴都取反向,则是前面两者的叠加,改变手性+旋转。
左右手坐标系的转换在图形学开发中经常出现,例如OpenGL使用右手坐标系,Unity使用左手坐标系。下文所述右手坐标系即是OpenGL坐标系,左手坐标系即是Unity坐标系。
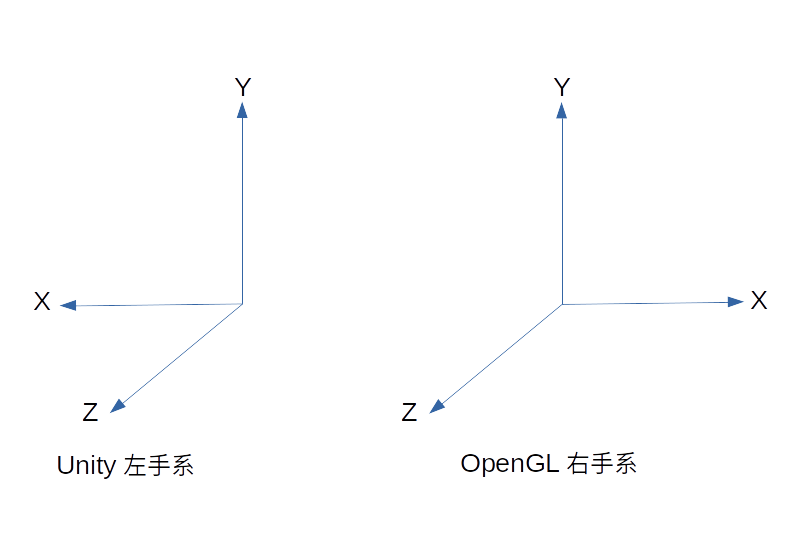
左手坐标系下有一个点$P_l=(x,y,z)^T$,则在右手坐标系下,该点应该表示为$P_r=(-x,y,z)^T$。
假设空间中有变换矩阵
$$S=\begin{bmatrix}
-1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{bmatrix}=S^{-1}$$
则左右手坐标系下点的变换即可用$S$来表示,即
$$
P_l = S \cdot P_r \\
P_r = S \cdot P_l
$$
假设空间中有旋转矩阵$R$和平移向量$T$,世界坐标系下有点$P_w$,对应相机坐标系下有点$P_c$,则有
$$
P_c = R \cdot P_w + T
$$
假设$P_c$、$P_w$、$R$、$T$均定义在右手坐标系下,${P_c}^{’}$、${P_w}^{’}$、${R}^{’}$、${T}^{’}$分别为上述变量在左手坐标系下的定义,即
$$
P_c = R \cdot P_w + T \\
{P_c}^{’} = {R}^{’} \cdot {P_w}^{’} + {T}^{’}
$$
左右手坐标系下位置的变换我们已经知道,即${P}^{’}=S \cdot P$,则有
$$
{P_c}^{’} = {R}^{’} \cdot {P_w}^{’} + {T}^{’} \rightarrow \\
S \cdot {P_c} = {R}^{’} \cdot S \cdot {P_w} + {T}^{’} \rightarrow \\
{P_c} = {S}^{-1} \cdot {R}^{’} \cdot S \cdot {P_w} + {S}^{-1} \cdot {T}^{’}
$$
已知右手坐标系下$P_c = R \cdot P_w + T$,故有左右手坐标系下旋转矩阵和平移向量的的转换
$$
R = S^{-1} \cdot R^{’} \cdot S = S \cdot R^{’} \cdot S \\
T = S^{-1} \cdot {T}^{’} = S \cdot {T}^{’}
$$
以上

